Answer:
179 units
Step-by-step explanation:
The computation of the economic order quantity is shown below:

where,
Annual demand = 1,200 cases
Ordering cost = $40
And, the annual carrying cost is $3 per case
Now placing these values to the above formula
So, the optimal order quantity is
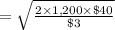
= 179 units
Hence, the optimal order quantity is 179 units