Question

A roulette wheel has the numbers 1 through 36, 0, and 00. A bet on two numbers pays 17 to 1 (that is, if you bet $1 and one of the two numbers you bet comes up, you get back your $1 plus another $17). How much do you expect to win with a $1 bet on two numbers

Answer 1

-$0.05

Explanation:

The computation is shown below:

The loss case = -1

The win case = 11 + 17 + 1 = 17

Now the number of pairs could be formed from (1 to 356, 0, 00) i.e.

`= (38!)/(2!36!)`

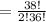
= 703

Now

Pr (x = 17) is

`= (1*37)/(703)\\\\ = (37)/(703)`

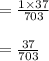
And, Pr (x = -1) is

`= 1 - (37)/(703)\\\\ = (666)/(703)`

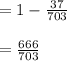
Now

E(x) = (-1) Pr (x = -1) + (17) Pr (x = 17)

`= -1 * (666)/(703) + 17 * (37)/(703) \\\\ = (-37)/(703)`

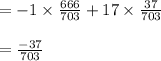
= -$0.05

hence, the -$0.05 would be expected to win that associated with a $1 bet on two numbers