Question

10 of 11 Review | Constants A planet moves in an elliptical orbit around the sun. The mass of the sun is Ms. The minimum and maximum distances of the planet from the sun are R1 and R2, respectively.

Using Kepler's 3rd law and Newton's law of universal gravitation, find the period of revolution P of the planet as it moves around the sun. Assume that the mass of the planet is much smaller than the mass of the sun. Use G for the gravitational constant. Express the period in terms of G, M, R1, and R2.
P =__________

Answer 1

T² = (π² / 2G M_{s}) (R₁ + R₂)³

Step-by-step explanation:

Let's use Newton's second law where the force is the universal gravitational force

F = m a

the acceleration is centripetal

a = v² / r

the out of gravitational universal is

F = G
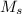`M_(s)` m / r²

we substitute

G M_{s} m / r² = m v² / r

G M_{s} / r = v²

the planet's speed in orbit is

v = d / T

v = 2π r / T

we substitute

G M_{s}/ r = 4π² r² / T²

T² = 4π² / G M_{s} r³

In the case of an elliptical orbit the distance r is the length of the semi-major axis, see attached for the nomenclature

T² = 4π² / G M_{s} a³

indicates that the minimum distance is R₁ = a -c and the maximum distance is R₂ = a + c, let's add these two expressions

R₁ + R₂ = 2 a

we substitute in the equation of the period

T² = 4π²/ G M_{s} (R₁ + R₂)³/2³

T² = (π² / 2G M_{s}) (R₁ + R₂)³