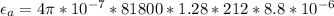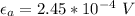Answer:
The amplitude of the induced emf is
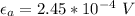
Step-by-step explanation:
From the question we are told that
The area is
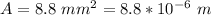
The number f turns per cm is
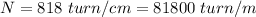
The current is
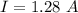
The angular frequency is
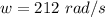
Generally the amplitude of the induced emf is mathematically represented as
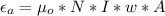
Where
 is the permeability of free space with value
is the permeability of free space with value
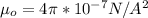
=>