Question

A computer retail store has 15 personal computers in stock. A buyer wants to purchase 3 of them. Unknown to either the retail store or the buyer, 3 of the computers in stock have defective hard drives. Assume that the computers are selected at random.

(a) In how many different ways can the 4 computers be chosen?
(b) What is the probability that exactly one of the computers will be defective?
(c) What is the probability that at least one of the computers selected is defective?

Answer 1

a. 1365 ways

b. Probability = 0.4096

c. Probability = 0.5904

Step-by-step explanation:

Given

PCs = 15

Purchase = 3

Solving (a): Ways to select 4 computers out of 15, we make use of Combination formula as follows;

`^nC_r = (n!)/((n-r)!r!)`

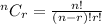
Where
`n = 15\ and\ r = 4`

`^(15)C_4 = (15!)/((15-4)!4!)`

`^(15)C_4 = (15!)/(11!4!)`

`^(15)C_4 = (15 * 14 * 13 * 12 * 11!)/(11! * 4 * 3 * 2 * 1)`

`^(15)C_4 = (15 * 14 * 13 * 12)/(4 * 3 * 2 * 1)`

`^(15)C_4 = (32760)/(24)`

`^(15)C_4 = 1365`

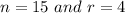
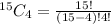
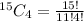
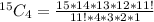
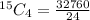
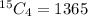
Hence, there are 1365 ways

Solving (b): The probability that exactly 1 will be defective (from the selected 4)

First, we calculate the probability of a PC being defective (p) and probability of a PC not being defective (q)

From the given parameters; 3 out of 15 is detective;

So;

`p = 3/15`

`p = 0.2`

`q = 1 - p`

`q = 1 - 0.2`

`q = 0.8`

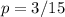
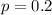
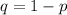
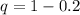
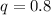
Solving further using binomial;

`(p + q)^n = p^n + ^nC_1p^(n-1)q + ^nC_2p^(n-2)q^2 + .....+q^n`

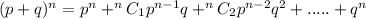
Where n = 4

For the probability that exactly 1 out of 4 will be defective, we make use of

`Probability = ^nC_3pq^3`

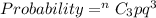
Substitute 4 for n, 0.2 for p and 0.8 for q

`Probability = ^4C_3 * 0.2 * 0.8^3`

`Probability = (4!)/(3!1!) * 0.2 * 0.8^3`

`Probability = 4 * 0.2 * 0.8^3`

`Probability = 0.4096`

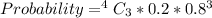
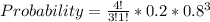
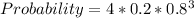
Solving (c): Probability that at least one is defective;

In probability, opposite probability sums to 1;

Hence;

Probability that at least one is defective + Probability that at none is defective = 1

Probability that none is defective is calculated as thus;

`Probability = q^n`

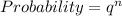
Substitute 4 for n and 0.8 for q

`Probability = 0.8^4`

`Probability = 0.4096`

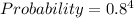
Substitute 0.4096 for Probability that at none is defective

Probability that at least one is defective + 0.4096= 1

Collect Like Terms

Probability = 1 - 0.4096

Probability = 0.5904