Answer:
the probability that more than 70% of customers in the sample will need additional maintenance is 0.0371
Explanation:
From the information given:
we are to determine the probability that more than 70% of customers in the sample will need additional maintenance
In order to achieve that, let X be the random variable that follows a binomial distribution.
Then X
 Bin(48, 0.6)
Bin(48, 0.6)
However 70% of 48 samples is
= 0.7 × 48 = 33.6
 34
34
Therefore, the required probability is:
= P(X> 34)

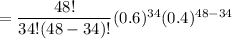

= 0.03709524328
 0.0371
0.0371