Answer:
The length and width of the parking lot are
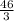 meters and
meters and
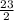 meters, respectively.
meters, respectively.
Explanation:
The surface formula (
 ) for the rectangular parking lot is represented by:
) for the rectangular parking lot is represented by:
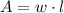
Where:
 - Width of the rectangle, measured in meters.
- Width of the rectangle, measured in meters.
 - Length of the rectangle, measured in meters.
- Length of the rectangle, measured in meters.
Since, surface formula is a second-order polynomial, in which each binomial is associated with width and length. If
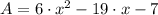 , the factorized form is:
, the factorized form is:
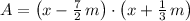
Now, let consider that
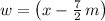 and
and
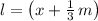 , if
, if
 , the length and width of the parking lot are, respectively:
, the length and width of the parking lot are, respectively:
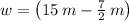
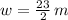
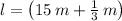
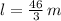
The length and width of the parking lot are
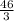 meters and
meters and
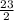 meters, respectively.
meters, respectively.