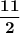Answer:
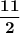
Explanation:
Given the geometric series:

To find:
Sum of series upto 5 terms using the geometric series formula = ?
Solution:
Formula for sum of a n terms of a geometric series is given as:
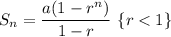
 is the first term of the geometric series
is the first term of the geometric series
 is the common ratio between each term (2nd term divided by 1st term or 3rd term divided by 2nd term ..... ).
is the common ratio between each term (2nd term divided by 1st term or 3rd term divided by 2nd term ..... ).
Here:

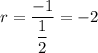

So, applying the formula for given values:
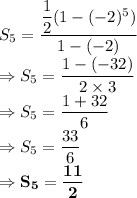
So, the answer is