Question

In an examination of purchasing patterns of shoppers, a sample of 36 shoppers revealed that they spent, on average, $50 per hour of shopping. Based on previous years, the population standard deviation is $4.80 per hour of shopping. Assuming that the amount spent per hour of shopping is normally distributed, calculate a 90% confidence interval.

Answer 1

the 90% confidence interval is ( 48.684 , 51.316 )

Explanation:

Given that :

the sample size = 36

Sample Mean = 50

standard deviation = 4.80

The objective is to calculate a 90% confidence interval.

At 90% confidence interval ;

the level of significance = 1 - 0.9 = 0.1

The critical value for
`z_(\alpha/2) = z_(0.1/2)`

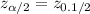
`= z_(0.05)` = 1.645

The standard error S.E =
`(\sigma)/(√(n))`

=
`(4.8)/(√(36))`

`=(4.8)/(6)`

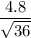
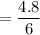
= 0.8

The Confidence interval level can be computed as:

`\bar x \ \pm z * \ ( \sigma )/(√(n))`

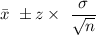
For the lower limit :

`\bar x \ - z * \ ( \sigma )/(√(n))`

`=50 \ - 1.645 * \ ( 4.8 )/(√(36))`

`=50 \ - 1.645 * \ 0.8 }}`

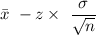
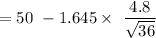
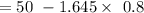
=50 - 1.316

= 48.684

For the upper limit :

`\bar x \ - z * \ ( \sigma )/(√(n))`

`=50 \ + 1.645 * \ ( 4.8 )/(√(36))`

`=50 \ + 1.645 * \ 0.8 }}`

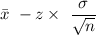
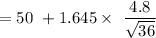
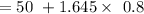
=50 + 1.316

= 51.316

Thus, the 90% confidence interval is ( 48.684 , 51.316 )