Answer:
(a) Approximately 68 % of women in this group have platelet counts within 1 standard deviation of the mean, or between 195.5 and 319.7.
(b) Approximately 99.7% of women in this group have platelet counts between 71.3 and 443.9.
Explanation:
We are given that the blood platelet counts of a group of women have a bell-shaped distribution with a mean of 257.62 and a standard deviation of 62.1
Let X = the blood platelet counts of a group of women
So, X ~ Normal(
 )
)
Now, the empirical rule states that;
- 68% of the data values lie within the 1 standard deviation of the mean.
- 95% of the data values lie within the 2 standard deviations of the mean.
- 99.7% of the data values lie within the 3 standard deviations of the mean.
(a) The approximate percentage of women with platelet counts within 1 standard deviation of the mean, or between 195.5 and 319.7 is 68% according to the empirical rule.
(b) The approximate percentage of women with platelet counts between 71.3 and 443.9 is given by;
z-score of 443.9 =

=
 = 3
= 3
z-score of 71.3 =

=
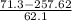 = -3
= -3
So, approximately 99.7% of women in this group have platelet counts between 71.3 and 443.9.