Answer:
λ = 102.78 nm
This radiation is in the UV range,
Step-by-step explanation:
Bohr's atomic model for the hydrogen atom states that the energy is
E = - 13.606 / n²
where 13.606 eV is the ground state energy and n is an integer
an atom transition is the jump of an electron from an initial state to a final state of lesser emergy
ΔE = 13.606 (1 /
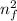- 1 / n_{i}^{2})
the so-called Lyman series occurs when the final state nf = 1, so the second line occurs when ni = 3, let's calculate the energy of the emitted photon
DE = 13.606 (1/1 - 1/3²)
DE = 12.094 eV
let's reduce the energy to the SI system
DE = 12.094 eV (1.6 10⁻¹⁹ J / 1 ev) = 10.35 10⁻¹⁹ J
let's find the wavelength is this energy, let's use Planck's equation to find the frequency
E = h f
f = E / h
f = 19.35 10⁻¹⁹ / 6.63 10⁻³⁴
f = 2.9186 10¹⁵ Hz
now we can look up the wavelength
c = λ f
λ = c / f
λ = 3 10⁸ / 2.9186 10¹⁵
λ = 1.0278 10⁻⁷ m
let's reduce to nm
λ = 102.78 nm
This radiation is in the UV range, which occurs for wavelengths less than 400 nm.