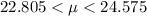Question

Refer to the accompanying​ TI-83/84 Plus calculator display of a​ 95% confidence interval. The sample display results from using a simple random sample of the amounts of tar​ (in milligrams) in cigarettes that are all king​ size, non-filtered,​ non-menthol, and​ non-light. Express the confidence interval in the format of E.

(23.305,25.075)
mean = 23.69
n = 30
The confidence interval is__?__ + or -___?___.

Answer 1

`22.805 < \mu < 24.575\\`

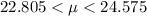
Explanation:

Given parameters

Z interval E = (23.305,25.075)

mean xbar = 23.69

number of samples n = 30

Required

we are to find the confidence interval for the Z interval given.

The formula for finding the confidence interval is expressed as shown below;

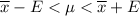`\overline x - E < \mu < \overline x + E` where;

xbar is the mean = 30

E is the margin of error

`E = (U-L)/(2)`

U = upper limit = 23.305

L = lower limit = 25.075

`E = (25.075-23.305)/(2)\\E = (1.77)/(2)\\E = 0.885`

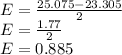
The confidence interval is therefore expressed as
`23.69 - 0.885 < \mu < 23.69+ 0.885\\22.805 < \mu < 24.575\\`

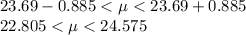
Hence the confidence interval is expressed as
`22.805 < \mu < 24.575\\`