Answer:
y = 6
Explanation:
Given a parallelogram ABCD with diagonals AC and BD.
Kindly refer to the diagram attached for the given parallelogram.
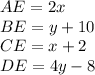
To find:
The value of y = ?
Solution:
First of all, let us consider a property of parallelogram and its diagonals.
The intersecting point of diagonals of a parallelogram bisect the diagonals in two equal parts.
Let us consider the given parallelogram ABCD which has its diagonals BD and AC intersecting at point E.
As per the property stated above:
AE = CE and
DE = BE
Putting the values of AE, CE, DE and BE as given in the question statement and solving for
 and
and
 :
:
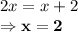
and
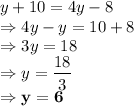
So, the answer is:
y = 6