Question

Given f(x) = -2x^2 + 4, determine the slope of the secant line over the interval [-1, 2].

Answer 1

Answer: -2

Explanation:

We know that the slope of a secant line over a interval [a,b] is given by :-

`m=(f(b)-f(a))/(b-a)`

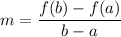
Given f(x) =
`-2x^2 + 4`

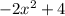
Then, the slope of the secant line over the interval [-1, 2] is given by :-

`m=(f(2)-f(-1))/(2-(-1))\\\\=((-2(2)^2+4)-(-2(-1)^2+4))/(2+1)\\\\=((-2(4)+4)-(-2(1)+4))/(3)\\\\=((-8+4)-(-2+4))/(3)\\\\=(-4-2)/(3)\\\\=(-6)/(3)\\\\=-1`

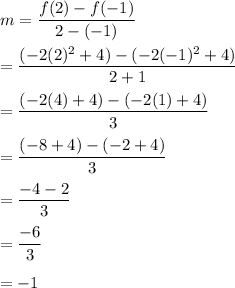
Hence, the slope of the secant line over the interval [-1, 2] is -2.