Question

A teacher wanted to know how well the gifted students in here class perform relative to her other classes. She administers a standardized test with a mean of 50 and a standard deviation of 10. A student scores of 55, what percent of students have a higher score than hers

Answer 1

Answer: 30.85%.

Explanation:

Let X denotes the score of random student.

Given:
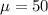`\mu = 50` and
`\sigma=10`

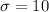
We assume that scores are normally distributed.

Then , the probability that a a student score higher than 55:

`P(X>55)=P((X-\mu)/(\sigma)>(55-50)/(10))\\\\=P(Z>0.5) \ \ [Z=(X-\mu)/(\sigma)]\\\\=1-P(Z<0.5)\\\\=1-0.6915\ [\text{By p-value table for z}]\\\\= 0.3085`

Hence, the percent of students have a higher score than hers is 30.85%.