Answer:
The area of the triangle is 24
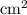 .
.
Explanation:
We are given that the length of the base of a right-angle triangle ABC is 6 cm and the length of the hypotenuse is 10 cm.
And we have to find the area of the triangle.
As we know that the area of the triangle is given by the following formula;
Area of the triangle =
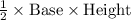
Firstly, we will find the height (perpendicular) of the triangle ABC bu using the Pythagoras Theorem.
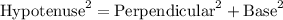
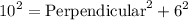
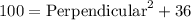
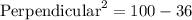
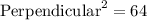
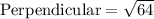 = 8 cm.
= 8 cm.
Now, the area of the triangle =
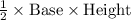
=
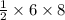
= 24
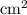
Hence, the area of the triangle is 24
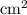 .
.