Answer:
The pints of each of the two existing types of drinks are 22 and 88 respectively.
Explanation:
We are given that the Royal Fruit Company produces two types of fruit drinks. The first type is 70% pure fruit juice, and the second type is 95% pure fruit juice. The company is attempting to produce a fruit drink that contains 90% pure fruit juice.
Let the first type of fruit drink pints in the mixture be 'x' and the second type of fruit drink pints in the mixture be 'y'.
So, according to the question;
- The first condition states that we have to make 110 pints of a mixture of two types that is pure fruit juice, that means;
x + y = 110
x = 110 - y ---------------- [equation 1]
- The second condition states that the first type is 70% pure fruit juice, and the second type is 95% pure fruit juice, that means;
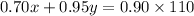
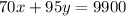
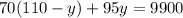
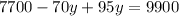

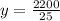
y = 88
Now, putting the value of y in equation 1 we get;
x = 110 - y
x = 110 - 88 = 22
Hence, the pints of each of the two existing types of drinks are 22 and 88 respectively.