Question

Give an example of an exponential function that includes the following transformations: o Vertical Compression o Reflection in the y-axis o Horizontal Stretch o Horizontal Translation to the left o Vertical Translation down

Answer 1

Explanation:

A transformation may be defined as taking a basic function and then changing it slightly with the predetermined methods. This changes will cause the required graph of that function to shift, move or stretch, which depends on the type of the transformation.

For example:

Let a function be :
`$f(x)= B^x$`

For any constants m and n, the function
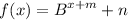`$f(x)= B^(x+m)+n$` shifts the parent function.

- vertically n units and in same direction of the sign of n.

- horizontally m units and towards the opposite direction of the sign of m.

- The y-intercept becomes (
`$0, b^m+n$`)

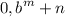- The horizontal asymptote becomes y = n.

- the reflection about x -axis becomes
`$f(x)=- B^x$`