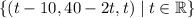There are infinitely many solutions for x, y and z.
By elimination, we have
(2x + 3y + 4z) - 2 (x + y + z) = 100 - 2•30
⇒ y + 2z = 40
and
(2x + 3y + 4z) - 3 (x + y + z) = 100 - 3•30
⇒ -x + z = 10
If we let z = t for some real number t, then
y + 2z = 40 ⇒ y = 40 - 2t
-x + z = 10 ⇒ x = t - 10
so any solution to the system is a point belonging to the set