Answer:

m<CQF = 32°
m<AQE = 32°
Explanation:
m<CQB = m<CQA = 90° (right angle)
m<CQB = m<CQF + m<FQB
m<CQF = 3x + 2
m<FQB = 58°
Therefore,
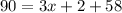
Solve for x:

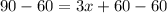

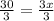
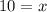

m<CQF = 3x + 2
Plug in the value of x to find m<CQF
m<CQF = 3(10) + 2 = 30 + 2
m<CQF = 32°
m<CQF and m<AQE are vertical opposite angles, therefore, they are congruent.
Thus,
m<AQE = 32°