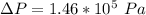Answer:
The pressure difference is
Step-by-step explanation:
From the question we are told that
The density is
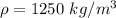
The speed at location 1 is
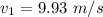
The diameter at location 1 is

The diameter at location 2 is
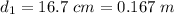
The height at location 1 is
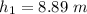
The height at location 2 is
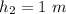
Generally the cross- sectional area at location 1 is mathematically represented as

=>
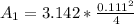
=>
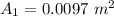
Generally the cross- sectional area at location 2 is mathematically represented as
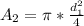
=>
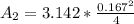
=>
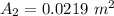
From continuity formula
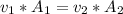
=>
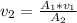
=>
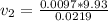
=>
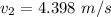
Generally according to Bernoulli's theorem
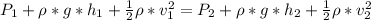
=>

=>
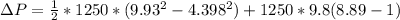
=>