Answer:
The angle is

Step-by-step explanation:
From the question we are told that
The mass of the crate is
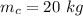
The coefficient of static friction is

The coefficient of kinetic friction is
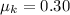
Generally for the the crate not to slip , the static frictional must be equal to the force driving the truck
i.e
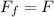
Now since we are considering a slope that static frictional force is mathematically represented as
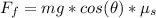
While the force driving the truck is mathematically represented as
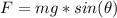
Here mg is the weight of the crate so
So
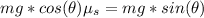
=>
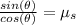
=>
![\theta = tan ^(-1) [\mu_s ]](https://img.qammunity.org/2021/formulas/physics/college/vjmy0s9xqwx67csymqask9rm23jlq3bgy3.png)
=>
![\theta = tan ^(-1) [0.40 ]](https://img.qammunity.org/2021/formulas/physics/college/4uztd88mwr6ugbhool2i6zvc6lzw6hwudl.png)
=>

A diagram show an illustration is on the first uploaded image