Answer:
The inductance of one conductor in the unstretched cord is 0.7849 μH
Step-by-step explanation:
Given;
number of turns of the coil, N = 52 turns
diameter of the coil, d = 1.30 cm
radius of the coil, r = d/2 = 1.30 cm / 2 = 0.65 cm = 0.0065 m
length of the unstretched cord, l = 57.5 cm = 0.575 m
The inductance of one conductor in the unstretched cord is given by;

where;
μ₀ is permeability of free space = 4π x 10⁻⁷ m/A
A is area of coil, = πr² = π x (0.0065)² = 1.328 x 10⁻⁴ m²
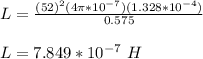
L = 0.7849 μH
Therefore, the inductance of one conductor in the unstretched cord is 0.7849 μH