Question

Whats the right answer?

Answer 1

A

Explanation:

Hello, I assume that the quadratic function f has real coefficients, so this is something like, a, b and c being real numbers

`f(x)=ax^2+bx+c`

If a complex number z is a zero of f ( meaning solution of f(x)=0) then

`\overline z` which is the conjugate of z is a zero too, because

`\text{if } f(z)=0=az^2+bz+c \text{ then}\\\\\overline {f(z)}=0=a\overline z ^2 +b \overline z + c\\\\\text{meaning } f(\overline z)=0`

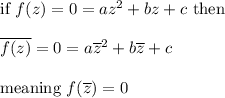
Here, we know that
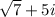`√(7)+5i` is a solution, so

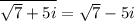`\overline {√(7)+5i}= √(7)-5i` is a solution too.

Thank you