Question

Give an expression for the answer using permutation​ notation, combination​ notation, factorial​ notation, or other operations. Then evaluate. Of the first questions on a​ test, a student must answer . Of the second ​questions, the student must answer . In how many ways can this be​ done?

Answer 1

This question is not complete. Let me explain the concept of combination and permutation.

Explanation:

The general formula for factorial is n! = n×(n - 1)×(n - 2)×...×2×1

0! = 1

Example 1:

How many different words can we make using the letters D, S, K and Z?

Solution:

We have 4 letters here.

Therefore, to get the possibility of the numbers, we will use:

4! = 4 x 3 x 2 x 1 = 24. We have 24 different words that can be made with the letters.

Permutation

The general formula for permutation is n P r = n! / (n - r)!

Example 2:

Find 5
`P_(3)`

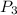
Solution: This will give 5!/(5-3)! = (5 x 4 x 3 x 2 x 1) / 2!

= 120 / 2 x 1 = 120 / 2 = 60

Combinations

The general formula for combination is n C r = n! / [ (n - r)! r! ]

Example 3:

Find 4
`C_(3)`

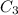
Solution: 4
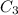`C_(3)` will give 4!/(4-3)!3! = (4 x 3 x 2 x 1) / 1!3!

= 24 / 1(3 x 2 x 1) = 24 / 6 = 4

Example 4: In Nigeria, the car number plate is formed by 4 digits from the digits 1, 2, 3, 4, 5, 6, 7, 8 and 9 followed by 3 letters from the alphabet. How many number plates will be formed if neither the digits nor the letters are repeated?

Solution: Note that we have 26 letters in the alphabet chart.

(9 P 4) × (26 P 3) = 9!/(9-4)! x 26!/(26-3)! = 47,174,400