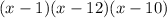Answer:
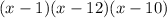
Explanation:
Given
Factorize:
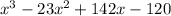
Required
Factorize
We start by checking for the factors of the given polynomial;
Check x - 1 = 0;
This implies that x = 1
Substitute 1 for x in
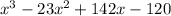
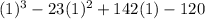
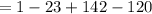
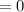
Since the result is 0, then x - 1 = 0 is a factor
Divide the polynomial by x - 1
(See attachment for long division)
The result is:
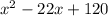
Hence, the factor is
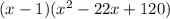
Expand the quadratic function
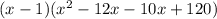
Factorize
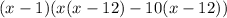
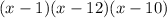
Hence;
Factorizing
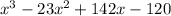 gives
gives