Question

The brazilian free-tailed bat can travel 99 miles per hour. after sunset, a colony of bats emerges from a cave and spreads out in a circular pattern. how long before these bats cover an area of 80,000 square miles? use pi = 3.14.

0.9 hours
1.6 hours
2.6 hours
5.1 hours

Answer 1

B: 1.6 hours

Explanation:

Answer 2

The colony of bats will take 1.612 hours to cover an area of 80,000 square miles.

Explanation:

As the colony of bats emerges from a cave and spreads out in a circular pattern, the area covered (
`A`) by the colony, measured in square miles, is represented by the following geometrical formula:

`A = \pi\cdot r^(2)`

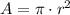
Where:

`r` - Distance of the bat regarding the cave, measured in miles.

In addition, each bat moves at constant speed and distance is represented by this kinematic formula:

`r = r_(o)+\dot r \cdot \Delta t`

Where:

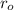`r_(o)` - Initial distance of the bat regarding the cave, measured in miles.

`\dot r` - Speed of the bat, measured in miles per hour.

`\Delta t` - Time, measured in hours.

The distance of the bat regarding the cave is now substituted and time is therefore cleared:

`A = \pi \cdot (r_(o)+\dot r \cdot \Delta t)^(2)`

`\sqrt{(A)/(\pi) }-r_(o) = \dot r \cdot \Delta t`

`\Delta t = (1)/(\dot r) \cdot \left(\sqrt{(A)/(\pi) }-r_(o) \right)`

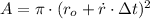
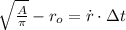
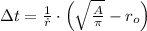
Given that
`\dot r = 99\,(mi)/(h)`,
`A = 80,000\,mi^(2)`,
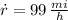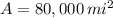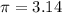`\pi = 3.14` and
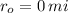`r_(o) = 0\,mi`, the time spent by the colony of bats is:

`\Delta t = \left((1)/(99\,(mi)/(h) ) \right)\cdot \left(\sqrt{(80,000\,mi^(2))/(3.14) }-0\,mi \right)`

`\Delta t \approx 1.612\,hours`

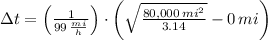
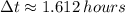
The colony of bats will take 1.612 hours to cover an area of 80,000 square miles.