Answer:
The minimum uncertainty in the velocity is 232.57 m/s.
Step-by-step explanation:
Given that,
Location of a particle with uncertainty = 0.13 nm
Mass of particle
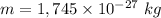
We need to calculate the minimum uncertainty in the velocity
Using heisenberg's uncertainty principle,
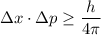
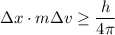
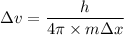
Put the value into the formula

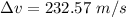
Hence, The minimum uncertainty in the velocity is 232.57 m/s.