Question

Determine the equation of the circle graphed below.
screenshot below!

Answer 1

(x-1)² + (y-6)² = 4

Explanation:

From the circle, endpoints (horizontal) are (-1,6) and (3,6). We will use these points to find midpoint (center) of the circle.

Midpoint Formula:

`\displaystyle \large{\left((x_1+x_2)/(2), (y_1+y_2)/(2)\right )}`

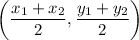
Determine:

• 
  `\displaystyle \large{(x_1,y_1) = (-1,6)}`
• 
  `\displaystyle \large{(x_2,y_2)=(3,6)}`

Hence:

`\displaystyle \large{\left((-1+3)/(2), (6+6)/(2)\right )}\\\displaystyle \large{\left((2)/(2) , (12)/(2)\right )}\\\displaystyle \large{\left( 1 ,6\right )}`

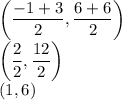
The midpoint (center) is (1,6). Next, find the radius which can be found by finding the distance between center and endpoint.

Determine:

• Center = (1,6) = (x1,y1)
• Endpoint = (3,6) = (x2,y2)

Distance Formula:

`\displaystyle \large{√((x_2-x_1)^2+(y_2-y_1)^2)}`

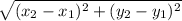
Therefore:

`\displaystyle \large{√((3-1)^2+(6-6)^2)}\\\displaystyle \large{√(2^2)}\\\displaystyle \large{√(4) = 2}`

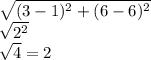
So our radius = 2.

Now we have:

• Center = (1,6)
• Radius = 2

Equation of Circle:

`\displaystyle \large{(x-h)^2+(y-k)^2=r^2}`

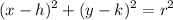
Where (h,k) is a center and r is radius:

Therefore, the solution is
`\displaystyle \large{(x-1)^2+(y-6)^2=4}`

Attachment is added for visual reference.