Question

3x - 4y = 19; 8x + y = 12
Are the equations parallel, perpendicular, or neither

Answer 1

Explanation:

Hey, there!

Let's check whether the lines are parallel, perpendicular or neither.

Fistly let's check of parallel ,

Let me tell you when two st. lines are paralle, then their slope are equal.

Given equation are,

3x - 4y = 9.........(i)

8x+y = 12 ..........(ii)

Now,

From equation (i)

`slope \: (m1) = ( - coffe. \: ofx)/(coffe. \: of \: y)`

`\: slope \: (m1) = ( - 3)/( - 4)`

`therefore \: slope \: (m1) = (3)/(4)`

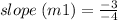
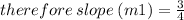
now, again slope from equation (ii).

`slope(m2) = ( - coffe.of \: x)/(coffe. \: of \: y)`

`slope \: (m2) = ( - 8)/(1)`

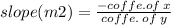
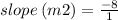
Therefore, the slope of equation (ii) is -8.

Since, Their slopes are not equal, they are not parallel.

Now, let's check for perpendicular,

To be perpendicular, slope (m1)× slope (m2)= -1

now,

`= (3)/(4) * - 8`

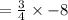
= 3×-2

= -6.

So, the equations are neither parallel nor perpendicular.

Hope it helps...