Answer:
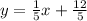
Explanation:
The slope of a line that is perpendicular to another will have an opposite-reciprocal slope. So, if the slope was -2, then the perpendicular slope would be
 .
.
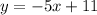
This is written in slope-intercept form:

m is the slope and b is the y-intercept. Find the opposite-reciprocal of the slope, -5:
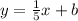
Now we need to find the y-intercept. For this, substitute the given points for its appropriate value:
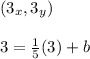
Solve for b:
Simplify multiplication:
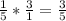
Insert:
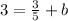
Subtract b from both sides:
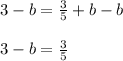
Subtract 3 from both sides:
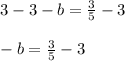
Simplify subtraction:
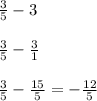
Insert:
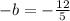
Multiply both sides by - 1 to simplify b (it can be seen as -1b):

Insert:
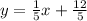
:Done