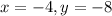Y = A system of equations. Y equals StartFraction one-half EndFraction x minus 6. X equals negative 4.X – 6 x = –4 What is the solution to the system of equations?

Question

asked Apr 18, 2021 147k views

1 Answer

James Cross · Answer 1 · 2021-04-23T12:49:21+0000

Answer:

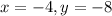x = -4, y =-8 is the solution to the system of equations.

Explanation:

Given the system of equations as:

y= (1)/(2)x-6

and

x =-4

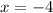
To find:

The solution to the system of equations = ?

Solution:

Here, we are given two equations and two variables i.e.
and
.

So, we can solve the system of equations for the values of
and
.

Let us first consider the 2nd equation.

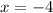x =-4 we already have the value of
.

Now, let us put the value of
in the 1st equation to find the value of
.

y= (1)/(2)x-6

$\Rightarrow y= (1)/(2)* (-4)-6\\\Rightarrow y= -(1)/(2)* 4-6\\\Rightarrow y= -2-6\\\Rightarrow \bold{y =-8}$

So, the solution to the system of equations is:

x = -4, y =-8