Question

At the Canterbury Dog Fair, 1/4 of the poodles are also show dogs and 1/7 of the show dogs are poodles. What is the least possible number of dogs at the fair?

Answer 1

10

Explanation:

Let the total number of poodles =
`x`

Let the total number of show dogs =
`y`

`(1)/(4)` of the poodles are show dogs

and

`(1)/(7)` of the show dogs are poodles

`\therefore (1)/(4)x = (1)/(7) y`

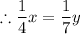
As per the question statement,
`x` must be divisible by 4 and

`y` must be divisible by 7.

And we have to find the least number of dogs.

So, least number divisible by 4 = 4 and

Least number divisible by 7 = 7

So, least values of
`x` i.e. poodles = 4 in which we have 1 show dog

Hence, 3 are not show dogs.

and least value of show dogs i.e.
`y` = 7 (it includes the one poodle which is also show dog).

So, least number of dogs at the fair = 7 + 3 = 10