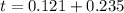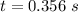Answer:
The time taken is
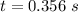
Step-by-step explanation:
From the question we are told that
The length of steel the wire is
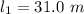
The length of the copper wire is

The diameter of the wire is
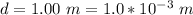
The tension is
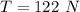
The time taken by the transverse wave to travel the length of the two wire is mathematically represented as
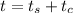
Where
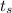 is the time taken to transverse the steel wire which is mathematically represented as
is the time taken to transverse the steel wire which is mathematically represented as
![t_s = l_1 * [ \sqrt{ (\rho * \pi * d^2 )/( 4 * T) } ]](https://img.qammunity.org/2021/formulas/physics/college/2w8okwxr11p66u5n92c3m4zykcil52lsw0.png)
here
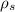 is the density of steel with a value
is the density of steel with a value
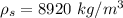
So
![t_s = 31 * [ \sqrt{ (8920 * 3.142* (1*10^(-3))^2 )/( 4 * 122) } ]](https://img.qammunity.org/2021/formulas/physics/college/kknptfsho3nqkgh5xdd5zf4xbi9d78jm2h.png)
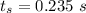
And
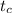 is the time taken to transverse the copper wire which is mathematically represented as
is the time taken to transverse the copper wire which is mathematically represented as
![t_c = l_2 * [ \sqrt{ (\rho_c * \pi * d^2 )/( 4 * T) } ]](https://img.qammunity.org/2021/formulas/physics/college/s0s9npcpma8s7sgfeary2m44jmxd9hylpe.png)
here
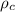 is the density of steel with a value
is the density of steel with a value
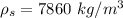
So
![t_c = 17 * [ \sqrt{ (7860 * 3.142* (1*10^(-3))^2 )/( 4 * 122) } ]](https://img.qammunity.org/2021/formulas/physics/college/60vgulh0ved4j4zsuhe9hbgrc3bgw4p45d.png)

So