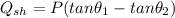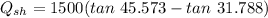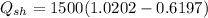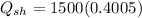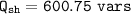Question

A circuit with a lagging 0.7 pf delivers 1500 watts and 2100VA. What amount of vars must be added to bring the pf to 0.85

Answer 1

`\mathtt{Q_(sh) = 600.75 \ vars}`

Step-by-step explanation:

Given that:

A circuit with a lagging 0.7 pf delivers 1500 watts and 2100VA

Here:

the initial power factor i.e cos θ₁ = 0.7 lag

θ₁ = cos⁻¹ (0.7)

θ₁ = 45.573°

Active power P = 1500 watts

Apparent power S = 2100 VA

What amount of vars must be added to bring the pf to 0.85

i.e the required power factor here is cos θ₂ = 0.85 lag

θ₂ = cos⁻¹ (0.85)

θ₂ = 31.788°

However; the initial reactive power
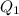`Q_1` = P×tanθ₁

the initial reactive power
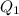`Q_1` = 1500 × tan(45.573)

the initial reactive power
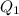`Q_1` = 1500 × 1.0202

the initial reactive power
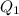`Q_1` = 1530.3 vars

The amount of vars that must therefore be added to bring the pf to 0.85

can be calculated as:

`Q_(sh) = P( tan \theta_1 - tan \theta_2)`

`Q_(sh) = 1500( tan \ 45.573 - tan \ 31.788)`

`Q_(sh) = 1500( 1.0202 - 0.6197)`

`Q_(sh) = 1500( 0.4005)`

`\mathtt{Q_(sh) = 600.75 \ vars}`