Question

a cannonball is fired with a speed of 76 m/s from the top of a cliff. It strikes the plane below with a speed of 89 m/s. if we neglect air friction, how high is the cliff

Answer 1

Assuming the cannonball is fired horizontally, its horizontal velocity stays at a constant 76 m/s. At the point it hits the ground, it has a speed of 89 m/s, so if its vertical velocity at that moment is
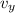`v_y`, we have

`89(\rm m)/(\rm s)=\sqrt{\left(76(\rm m)/(\rm s)\right)^2+{v_y}^2}\implies{v_y}^2\approx2145(\mathrm m^2)/(\mathrm s^2)`

(taking the negative square root because we take the downward direction to be negative)

Recall that

`{v_f}^2-{v_i}^2=2a\Delta x`

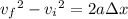
where
`v_i` and
`v_f` are the initial and final velocities, respectively;
`a` is the acceleration; and
`\Delta x` is the change in position of a body. In the cannonball's case, it starts with 0 vertical velocity and is subject to a downward acceleration with magnitude
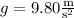`g=9.80(\rm m)/(\mathrm s^2)`. So we have

`2145(\mathrm m^2)/(\mathrm s^2)-0=-2g\Delta y\implies\Delta y\approx-109.44\,\mathrm m`

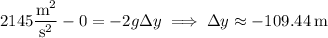
(which is negative because we take the cannonball's starting position at the top of the cliff to be the origin) so the cliff is about 109 m high.