Answer:
171 million
Explanation:
Given the exponential growth formula expressed as
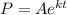 where P is the countrys population and t is the time.
where P is the countrys population and t is the time.
Initially in 1991, at t= 0, P = 147 million

If by 1998 it was 153 million, this means that the population is 153 million 7 years later i.e when t = 7, P = 153. On substituting into the formula to get the constant 'k';

To estimate the population in 2017, to number of years from 1991 to 2017 is 26 years. Hence we are to find the value of P given t = 27, A = 147 and k = 0.00574
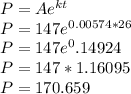
Hence the population in 2017 using exponential growth formula to the nearest million is 171 million.