Question

a 1.2 x 10^4 kg railroad car is coasting along a level, frictionless track at a constant speed of 25m/s, when a 3000 kg load is dropped vertically onto the car from above. What will its new speed be assuming the load stays on the car??

Answer 1

`20\; \rm m \cdot s^(-1)`.

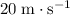Step-by-step explanation:

Because the track is level and frictionless, the net force on this car-load system will be zero in the horizontal direction. As a result, (by Newton's Second Law of mechanics,) the total momentum of this system in the horizontal direction will stay the same.

Momentum of the car-load system in the horizontal direction, before contact:

• Car:
  `m(\text{car}) \cdot v(\text{car, before}) = 1.2 * 10^(4)\; \rm kg * 25\; m \cdot s^(-1) = 3.0 * 10^(6)\; \rm kg \cdot m \cdot s^(-1)`.
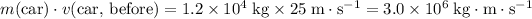• Load: zero (for it is dropped "vertically.")

Combine the two parts to obtain:
`p(\text{system, before}) = 3.0 * 10^(6)\; \rm kg \cdot m \cdot s^(-1)`.

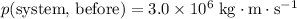Because the load stays on the car, the car and the load should have the same horizontal velocity after contact. Let
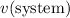`v(\text{system})` denote that velocity. Momentum of the system after contact:

• Car:
  `m(\text{car}) \cdot v(\text{car, after}) = 1.2 * 10^(4)\; \rm kg * (\mathnormal{v}(\text{system}))`.
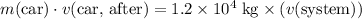• Load:
  `m(\text{load}) \cdot v(\text{load, after}) = 3000\; \rm kg * (\mathnormal{v}(\text{system}))`.

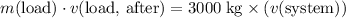Combine to obtain:

`p(\text{system, after}) =1.5* 10^(4)\; \rm kg * (\mathnormal{v}(\text{system}))`.

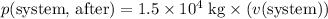Because the total momentum of the system will stay the same:

`\begin{aligned}&1.5* 10^(4)\; \rm kg * (\mathnormal{v}(\text{system}))\\ &= p(\text{system, after}) \\&= p(\text{system, before}) \\ &= 3.0* 10^(6)\; \rm kg \cdot m \cdot s^(-1)\end{aligned}`.

Solve for
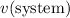`v(\text{system})` to obtain:

`v(\text{system}) = 20\; \rm m\cdot s^(-1)`.

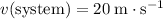In other words, the new velocity of the system would be
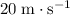`20\; \rm m \cdot s^(-1)`.