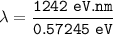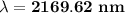Question

What is the wavelength of radiation emitted when an electron goes from the n = 7 to the n = 4 level of the Bohr hydrogen atom? Give your answer in nm.

Answer 1

the wavelength of radiation emitted is
`\mathbf{\lambda= 2169.62 \ nm}`

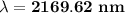
Step-by-step explanation:

The energy of the Bohr's hydrogen atom can be expressed with the formula:

`\mathtt{E_n =- (13.6\ ev)/(n^2)}`

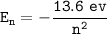
For n = 7:

`\mathtt{E_7 =- (13.6\ ev)/(7^2)}`

`\mathtt{E_7 =-0.27755 \ eV}`

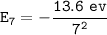
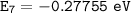
For n = 4

`\mathtt{E_4=- (13.6\ ev)/(4^2)}`

`\mathtt{E_4 =- 0.85\ eV}`

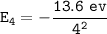
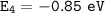
The electron goes from the n = 7 to the n = 4, then :

`\mathtt{E_7-E_4 = (-0.27755 - (-0.85) ) \ eV}`

`\mathtt{= 0.57245\ eV}`

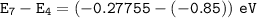
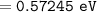
Wavelength of the radiation emitted:

`\mathtt{\lambda= (hc)/(0.57245 \ eV)}`

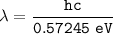
where;

hc = 1242 eV.nm

`\mathtt{\lambda= (1242 \ eV.nm )/(0.57245 \ eV)}`

`\mathbf{\lambda= 2169.62 \ nm}`