Answer:
a=-2, b=1.
Explanation:
1) according to the condition it is required to find the equation of line, which passes through points A(-3;7) and B(4;-7);
2) the equation of this line can be made up using the formula:

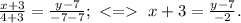
3) if to re-write the last equation, then
y=-2x+1;
4) finally, a= -2; b=1.