Question

Find the largest value of $n$ such that $5x^2+nx+48$ can be factored as the product of two linear factors with integer coefficients.

Answer 1

`n = 241`

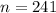
Explanation:

Given

`5x^2 + nx + 48`

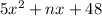
Required

Determine the highest value of n

From the given equation, 5 is a prime number;

So, the factors of x² is 5x and x or -5x and -x

Since
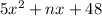`5x^2 + nx + 48` has all shades of positive terms, we'll make use of 5x and x

The factorized expression can then be:

`(5x + a)(x + b)`

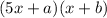
Open the brackets

`5x^2 + ax + 5bx + ab`

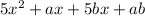
Equate this to the given expression

`5x^2 + ax + 5bx + ab = 5x^2 + nx + 48`

`5x^2 + (a + 5b)x + ab = 5x^2 + nx + 48`

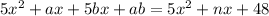
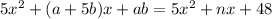
By direct comparison;

`5x^2 = 5x^2`

`(a + 5b)x = nx`

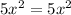
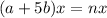
`a + 5b = n` ---- (1)

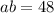`ab = 48` --- (2)

From (2) above, the possible values of a and b are:

`a = 1, b = 48`

`a = 2, b = 24`

`a = 3, b = 16`

`a = 4, c = 12`

`a = 6, b = 8`

`a = 8, b = 6`

`a = 12, b = 4`

`a = 16, b = 3`

`a = 24, b = 2`

`a = 48, b = 1`

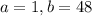
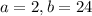
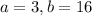
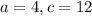
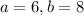
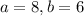
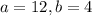
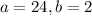
Of all these values; the value of a and b that gives the highest value of n is;

`a = 1, b = 48`

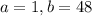
So;

Substitute 1 for a and 48 for b in (2)
`a + 5b = n`

`1 + 5 * 48 = n`

`1 + 240 = n`

`241 = n`

`n = 241`

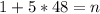
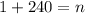
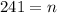
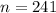
Hence, the largest value of n is 241