Answer:
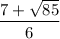 and
and
 .
.
Explanation:
(Replace
 with
with
 to avoid confusion with symbols in the quadratic equation.)
to avoid confusion with symbols in the quadratic equation.)
Notice that the equation
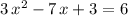 is quadratic with respect to the unknown
is quadratic with respect to the unknown
 . Rewrite the equation in standard form
. Rewrite the equation in standard form
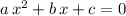 before applying the quadratic equation:
before applying the quadratic equation:
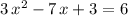 .
.
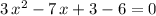 .
.
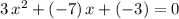 .
.
Thus, for the quadratic equation,
 ,
,
 , and
, and
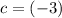 . Apply the quadratic equation to find the solutions:
. Apply the quadratic equation to find the solutions:
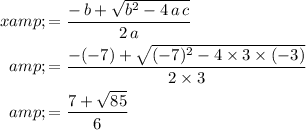 .
.
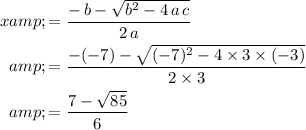 .
.