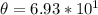Answer:
The angle is
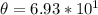
Step-by-step explanation:
From the question we are told that
The intensity of light emerging from the second polarizer is
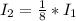
Now the light emerging from the first polarizer is
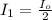
Where
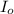 is the intensity of the unpolarized light
is the intensity of the unpolarized light
Now according to Malus law the intensity of light emerging from the second polarizer is mathematically represented as
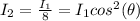
=>
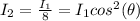
=>
![\theta = cos^(-1)[0.3536]](https://img.qammunity.org/2021/formulas/physics/college/jg4sehrqe8f9gktrlveyyqf8utyimp79c6.png)
=>
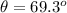
=>