Answer:
The distance between these points is approximately is 9.198 units.
Explanation:
Let be (5.5, 2.9) and (-3.5, 4.8) the location of the points in Cartesian plane. The straight line distance between both points (
 ) is determined by the Pythagorean Theorem, which is described below:
) is determined by the Pythagorean Theorem, which is described below:
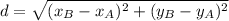
Where:
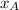 ,
,
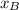 - Horizontal components of each point, dimensionless.
- Horizontal components of each point, dimensionless.
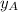 ,
,
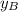 - Vertical components of each point, dimensionless.
- Vertical components of each point, dimensionless.
If
 and
and
 , the distance between these points is:
, the distance between these points is:
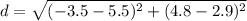
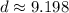
The distance between these points is approximately is 9.198 units.