Answer:
The time it will take for the ball to reach maximum height of 64 feet is 2 seconds
Explanation:
The given equation for the height, h, in feet the ball reaches is given by the function;
h(t) = -16·t² + 64·t
To reach maximum height,
 , we have;
, we have;
At
 , we have;
, we have;
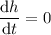
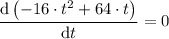
Which gives;
64 -32·t = 0
64 = 32·t
t = 64/32 = 2 seconds
Therefore, it will take 2 seconds for the ball to reach maximum height
The maximum height reached is given as follows;
h(2) = -16×2² + 64×2 = 64 feet
The time it will take for the ball to reach maximum height of 64 feet is 2 seconds.