Question

Evaluate plz plz plz help me i am soo confused

Answer 1

Hey there! I'm happy to help!

QUESTION 100

Here, we are looking for the number of permutations. A permutation is the number of possible arrangements you can make from a given set of things (order matters). If you have 6 kids standing in alphabetical order in line, that is one permutation. If you do reverse alphabetical order, that is a different permutation.

We are asked to find the number of permutations using the given format:

`_(n)P_(r)\\`

This is simply a representation of what we want to find. The P means we are looking for the number of permutations. The n is the total number of objects in the set (for example, if there were 26 kids we could choose from to make this 6 person line, n would be 26). The r is the number of things chosen from the set (in our line example, the r would be six because we are choosing 6 kids).

The formula for finding the number of permutations is
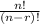`(n!)/((n-r)!)`. The ! is factorial, it means you multiply that number by every integer counting backwards towards 1. 6! is 6×5×4×3×2×1. There is an option to do this on your calculator, though.

Let's solve this problem.

`_(5)P_(4)=(5!)/((5-4)!)= (120)/(1) =120`

This means that there are 120 permutations.

QUESTION 101

Now we have a C. This is similar to permutations but with combinations order does not matter. With our line example, having the same six kids in alphabetical order is a different permutation than having it in backwards alphabetical order. With combinations, if you have those specific six kids, it is just one combination; the order does not matter.

The formula for combinations is
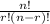`\frac {n!}{r!(n-r)!}`. Let's plug in our numbers and solve for this.

`_(8)C_(2)=(8!)/(2!(8-2)!) =(8!)/(2!(6!))=(40320)/(1440) =28`

QUESTION 102

Quick note: 0! is equal to 1. I don't really know why but there's probably proof somewhere.

`_(7)C_(0)=(7!)/(0!(7-0)!) =(7!)/(7!) =1`

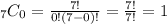
And I believe you already have Question 103 figured out.

4!=4×3×2×1=24

Have a wonderful day! :D