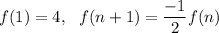Question

Which of the following functions describes the sequence 4, –2, 1, –12, 14, . . .? A. f(1) = 4, f(n + 1) = –2f(n) for n ≥ 1 B. f(1) = 4, f(n + 1) = f(n) – 2 for n ≥ 1 C. f(1) = 4, f(n) = 12f(n + 1) for n > 1 D. f(1) = 4, f(n) = –12f(n – 1) for n > 1

Answer 1

Answer: D.
`f(1) = 4,\ \ f(n+1)=(-1)/(2)f(n)`

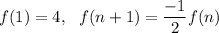
Explanation:

The given sequence:
`4, -2,1,(-1)/(2),\frac14,....`

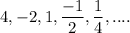
Here, first term:
`f(1)=4`

Second term:
`f(2)=-2`

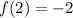
Third term :
`f(3)=(-1)/(2)`

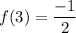
It can be observed that it is neither increasing nor decreasing sequence but having the common ratio.

Common ratio:
`r=(f(2))/(f(1))=(-2)/(4)=(-1)/(2)`

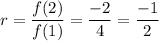
So,
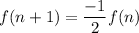`f(n+1)=(-1)/(2)f(n)` [as in G.P. nth term=
`a_(n+1)=ar^n`]

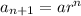Hence, correct option is D.
`f(1) = 4,\ \ f(n+1)=(-1)/(2)f(n)`