Question

What is the slope form equation?

Answer 1

You may already know that "y+MX+b" form called the slope-intercept form of the equation of a line. It is the same equation in a different form. The 'b' value called the y intercept is where the line crosses the y- axis

Explanation:

Answer 2

y= mx +c

Explanation:

The point- slope form of an equation is

y= mx +c, where m is the gradient and c is the y-intercept.

You can find the value of m by using the gradient formula.

`gradient = (y1 - y2)/(x1 - x2)`

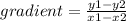
Then substitute the value of m found into the equation. Next substitute a pair of coordinates the line passes through to find the value of c. Substitute the value of c and you will obtain the point-slope form equation of the line.

Here's an example.

Point-slope form of an equation passing through (1, 2) and (5, 6).

① Finding gradient, m.

`m = (6 - 2)/(5 - 1) \\ m = (4)/(4) \\ m = 1`

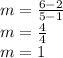
② Substitute value of m into equation.

y= 1x +c

y= x +c

③ Substitute a pair of coordinates.

when x=1, y=2,

2= 1 +c

c= 2 -1

c= 1

Thus the equation of the line is y= x +1.