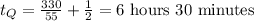Answer:
Train P :
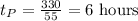
Train Q :
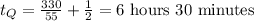
Explanation:
The formula to compute the distance traveled by a train is:

Here,
d = distance traveled
s = speed of the train
t = time taken
From the provided information:
Train P :
d = 330 km
s = x km/h
Then time taken is:

Train Q :
d = 330 km
s = (x - 5) km/h
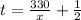
Both the trains traveled the same distance.
![x* (330)/(x)=(x-5)* [(330)/(x)+(1)/(2)]\\\\330=(330(x-5))/(x)+(x-5)/(2)\\\\330* 2x=[660(x-5)+x(x-5)]\\\\660x=660x-3300+x^(2)-5x\\\\x^(2)-5x-3300=0\\\\x^(2)+60x-55x-3300=0\\\\x(x+60)-55(x+60)=0\\\\(x-55)(x+60)=0\\\\x=55](https://img.qammunity.org/2021/formulas/mathematics/high-school/dypcy11wfwqujkuvwnnu4fvud09lgaoutq.png)
Compute the time taken by the two trains as follows:
Train P :
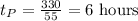
Train Q :