Question

A scale at a grocery store is made of a metal pan (of negligible mass) placed on an ideal spring. The spring has a force constant of 655 N/m. A customer gently rests 1.00 kgs of bananas and 2.00 kg of potatoes on the scale. When the 2.00 kg potatoes is suddenly removed, how high above the starting position do the bananas reach?

Answer 1

The ideal spring is 0.030 meters above the starting position.

Step-by-step explanation:

Let consider that spring is modelled by the Hooke's Law, which is represented by the following expression:

`F = k\cdot \Delta x`

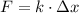
Where:

`F` - Force exerted on the ideal spring, measured in newtons.

`k` - Spring constant, measured in newtons per meter.

`\Delta x` - Spring elongation, measured in meters.

The elongation is now cleared:

`\Delta x = (F)/(k)`

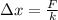
The initial force experimented by the spring is due to the weight of bananas and potatoes.

`F = (m_(b) + m_(p))\cdot g`

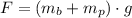
Where:

`m_(b)`,
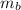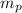`m_(p)` - Masses of bananas and potatoes, measured in kilograms.

`g` - Gravitational acceleration, measured in meters per square second.

If
`m_(b) = 1\,kg`,
`m_(p) = 2\,kg`,
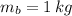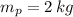`g = 9.807\,(m)/(s^(2))` and
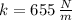`k = 655\,(N)/(m)`, the initial elongation of the ideal spring is:

`F = (1\,kg + 2\,kg)\cdot \left(9.807\,(m)/(s^(2)) \right)`

`F = 29.421\,N`

`\Delta x_(o) = (29.421\,N)/(655\,(N)/(m) )`

`\Delta x_(o) = 0.045\,m`

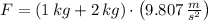
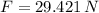
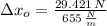
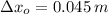
The final elongation is obtained after eliminating the influence of potatoes due to gravity. That is to say:

`F = m_(b)\cdot g`

`F = (1\,kg)\cdot \left(9.807\,(m)/(s^(2)) \right)`

`F = 9.807\,N`

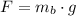
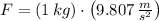
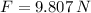
The final elongation of the ideal spring is:

`\Delta x_(f) = (9.807\,N)/(655\,(N)/(m) )`

`\Delta x_(f) = 0.015\,m`

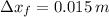
The displacement of the spring due to the removal of potatoes is:

`d = \Delta x_(o) - \Delta x_(f)`

`d = 0.045\,m-0.015\,m`

`d = 0.030\,m`

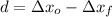
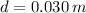
The ideal spring is 0.030 meters above the starting position.